2458번 키 순서

 플로이드 와샬 문제.

 

 플로이드 와샬은 모든 정점에서 모든 정점으로의 최단 경로를 구하는 알고리즘이다. 즉, 최단 경로가 존재한다는 것은 갈 수가 있다는 것이고 이 문제에서 그 말은 키를 비교할 수 있다는 것이다.

 

 이 문제의 예시 답은 1, 4번만 자신의 키 순서를 알고 있다. 

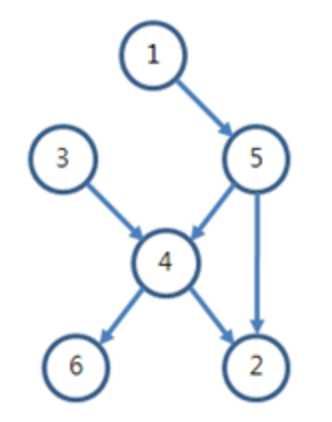
 플로이드 와샬을 실행하게 되면 4번은 2번과 6번에 갈 수 있고 1번과 3번, 그리고 5번은 모른다.

 이 상황에서

 1번을 기준으로 4번으로 가는 길이 존재하고

 3번을 기준으로 4번으로 가는 길이 존재하고

 5번을 기준으로 4번으로 가는 길이 존재한다면 

 4번의 키가 몇 번째인지 알 수 있다.

   

 

#include <iostream>
#define INF 987654321
#define MAX 501
 
using namespace std;
 
int N,M;
int map[MAX][MAX];
int ans;
 
void floydWarshall(){
    int d[MAX][MAX];
    
    for(int i=1;i<=N;i++){
        for(int j=1;j<=N;j++){
            d[i][j]=map[i][j];
        }
    }
    
    for(int k=1;k<=N;k++){
        for(int i=1;i<=N;i++){
            for(int j=1;j<=N;j++){
                if(d[i][k]+d[k][j]<d[i][j]){
                    d[i][j]=d[i][k]+d[k][j];
                }
            }
        }
    }
    
    // 플로이드 와샬을 실행하게 되면 4번은 2번, 6번에 갈 수 있다. 즉, 1번과 3번 그리고 5번을 모른다는 것이다.
    // 그렇다면
    // 1번을 기준으로 4번으로 가는 길이 존재하고
    // 3번을 기준으로 4번으로 가는 길이 존재하고
    // 5번을 기준으로 4번으로 가는 길이 존재한다면
    // 4번의 키가 몇 번째인지 알 수 있다.
    
    for(int i=1;i<=N;i++){ // 갈 수 있다면 0으로 표시, 즉 4번의 플로이드 와샬 값은 0 1 0 0 0 1 가 된다.
        for(int j=1;j<=N;j++){
            if(i!=j && d[i][j]==INF){
                if(d[j][i]!=INF){
                    d[i][j]=0;
                }
            }
        }
    }
 
    for(int i=1;i<=N;i++){
        int k=0;
        for(int j=1;j<=N;j++){
            if(d[i][j]==INF) {
                k=0;
                break;
            }
            else{
                k=1;
            }
        }
        ans+=k;
    }
    
    cout << ans << endl;
}
 
int main(){
    cin >> N >> M;
    
    for(int i=1;i<=N;i++){
        for(int j=1;j<=N;j++){
            map[i][j]=INF;
            if(i==j){
                map[i][j]=0;
            }
        }
    }
    
    for(int i=0;i<M;i++){
        int a,b;
        cin >> a >> b;
        map[a][b]=1;
    }
    
    floydWarshall();
}